Understanding Statistics
Guide to Interpreting Statistics
1. Interpreting Statistics: Introduction
As a teacher, you will not typically be expected to conduct your own statistical tests. When reading background research, however, you may encounter quantitative research in which other authors have used statistics to determine their findings.
This is an advanced guide to help you interpret the statistical tests used by others. The guide will take you through notation used in statistics, some commonly statistical tests, and a quiz to test your own interpretation of the statistics used in other research. If you are a complete newby to statistics, never fear: we provide some additional resources for you to review. A good research paper will also help you: by summarising the results and their implications in the abstract and at the beginning of the discussion.
2. Notation/Glossary
M: Mean, the average of your scores
N: total number in a sample
n: number in a subsample
r: correlation coefficient
b/β: regression coefficient
- Standard deviation: a standardized measurement of how far a score is from the mean
- Null hypothesis: a statement that predicts no statistically significant difference between two groups or individuals
- Effect size: a practical measure of the difference between two groups
- P-value: the probability of rejecting the null hypothesis when the null hypothesis is actually true
- Correlation coefficient: a number between -1 and 1 that indicates the strength and direction of a relationship between two variables
- Regression coefficient: a number between -1 and 1 (unless specified as unstandardised) that indicates the strength and direction of a relationship between two variables after accounting for the relationships of other variables. This coefficient provides information about whether one variable “predicts” another.
3. Statistical Tests
The most common tests you will come across are t-tests, analyses of variance (ANOVA) and chi—squared tests. These tests are used to calculate a test statistic such as t, F and χ2, which is then converted to a p-value using conversion tables or a computer program. P-values give us the most valuable information about the study by portraying how likely it is that your results have occurred by chance. Generally, p values of less than 0.05 (p < 0.05) are considered non-random or statistically significant, allowing you to reject the null hypothesis. However, this figure is set by the researcher and can therefore vary. Some common tests are tabulated below:
Test name |
Test Statistic Produced |
What does it do? |
Example |
Two sample (independent samples) t-test |
t |
Compares two independent samples (groups) from the same population. |
Comparing the IQs of boys and girls |
One-sample (paired) t-test |
t |
Compares two sets of data collected from a single group |
Comparing a group’s results on a test before and after a learning intervention |
One-way analysis of variance (ANOVA) |
F |
Compares three or more sets of data from a single group |
Comparing the results of a group on a test 2, 4 and 6 weeks after a learning intervention |
Two-way analysis of variance |
F |
Compares three or more sets of data from two independent groups |
Comparing the results of boys against girls on a test 2, 4 and 6 weeks after a learning intervention. |
Chi-squared test |
χ2 |
Tests the null hypothesis that the proportions of variables estimated from two independent samples are the same |
To determine whether the achievement of a high distinction is equally likely for an Australian resident as an International student |
Pearson’s r correlation coefficient |
r |
Assesses the strength of a straight line relationship between two variables |
To assess to what extent test scores in English and maths are correlated. |
Regression coefficient |
b/β |
Assesses the strength of a straight line relationship between two variables, after accounting for the relationship with other variables |
To assess the extent to which test scores in English are associated with reading enjoyment after accounting for gender, socioeconomic status, and working memory |
4. Test Statistics
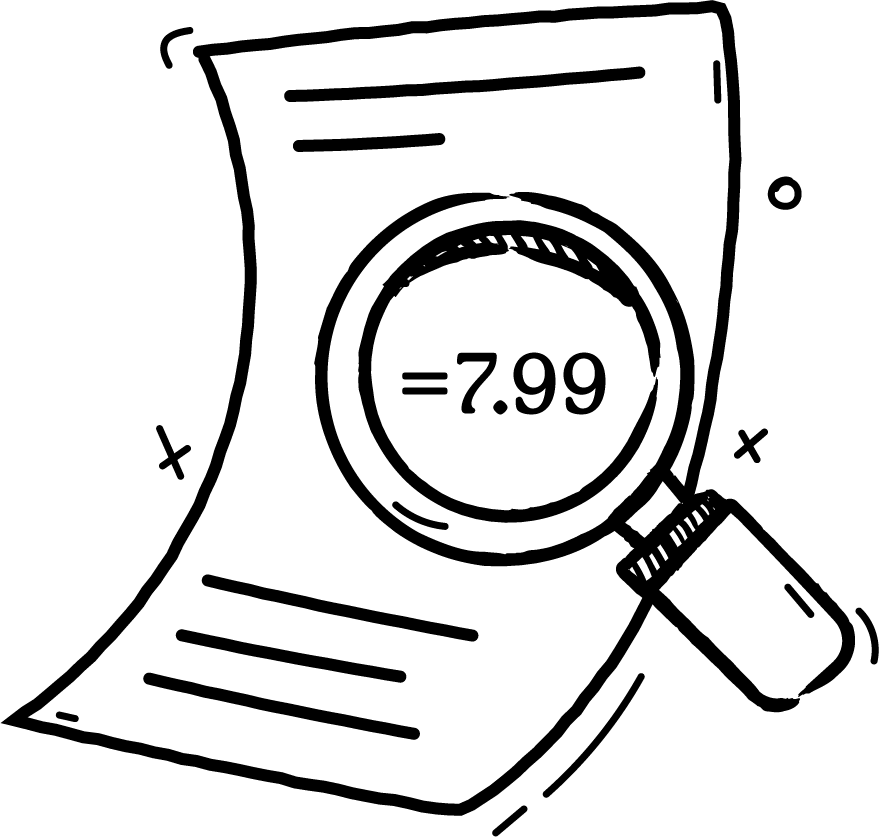
In journal articles, your test statistic will usually appear followed by numbers in brackets. This represents the number of participants or the degrees of freedom- don’t panic! The information that is valuable to you comes after the equals sign. Some examples include:
- Example 1: F(1, 39) =7.99 ß the test statistic here is 7.99
- Example 2: t(25)=2.05 ß the test statistic here is 2.05
Correlation coefficients (r) and regression coefficients (b/β) will lie between -1 and 1. The closer the value to -1 or 1, the stronger the relationship, values closer to 0 represent a weaker relationship. The same rules apply to both correlation and regression coefficients. Come examples include:
- Example 1: When height and weight are correlated, r=0.8, meaning there is a strong positive relationship; as height increases so does weight
- Example 2: When exercise frequency is correlated with resting heart rate, r=-0.8, meaning there is a strong negative relationship; as frequency of exercise increases, resting heart rate decreases
- Example 3: When height is correlated with IQ, r=0.1, meaning there is a weak positive relationship. As height increases, there is no obvious change in IQ. If the study was repeated, it is possible that a weak negative ‘r’ value could be obtained.
5. Effect Size
While test statistics converted to p-values are used to tell us whether or not there is a statistically significant difference between our data groups or a significant relationship, effect size is a measure of practical significance used to provide information about how big the difference or relationship is.
It is important to remember that significance and meaningfulness are different. We consider effect sizes because they tell us, relatively, how practically important the finding is and where we might see the largest effects.
Effect Size |
Mean Difference (Cohen’s d) |
Correlations (r) |
Regressions (β) |
How large is the difference between two groups?**Can also use g or η2 |
How large is the association between two variables? |
How large is the association between two variables, after accounting for the relationship with other variables |
|
Not meaningful/interpret with caution |
< .20 |
< .10 |
< .05 |
Small but meaningful |
.20 |
.10 – .30 |
.05 – .10 |
Moderate |
.50 |
.30 – .50 |
.10 – .25 |
Large |
.80 |
> .50 |
> .25 |
** This table refers to absolute values
Practice Decoding Results Sections
This quiz has three (3) questions and will help you determine your ability to undestand the results sections of various studies. There are no final grades, it’s just for you to practice. Give it a try!